Friction Preset
FrictionPreset is a ScriptableObject containing data about the friction properties of a tire.
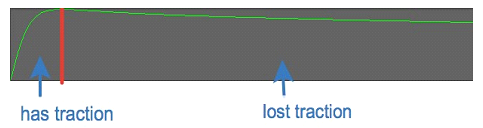
WheelController's friction is slip-based. Tire always has some slip but it is very small under normal conditions – always near the left side of the curve below.
Image above shows friction curve with slip on the X axis and friction on the Y axis. Part of the curve on the left side marked as “has traction” is where tires normally operate, and part on the right side is where the tire lost traction. Depending on the shape of the curve vehicle will act differently upon losing traction. Here are parameters of the curve and how they affect handling:
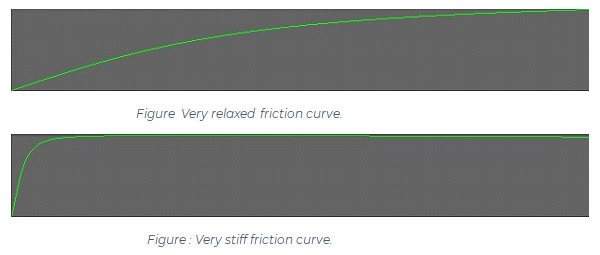
B (stiffness)– With higher value curve will be faster to reach peak value meaning it will be steeper. This means that wheel will require less slip to lose traction and such vehicle will be more unstable – i.e. spin out more easily. With lower values of stiffness vehicle will be more stable and harder to spin but with very low value it will start to act as if on ice.
C (shape)– While stiffness determines where the peak will be, shape determines how strong the knee in the curve will be. High shape value will make it pointy while low value will make it flatter.D (peak)– The higher it is the more traction wheel will have. It does exactly the same thing as Slip Coefficient field does. To simplify, resultant friction is equal to peak value times slip coefficient times some other values - this means that if peak is set to 0.5 and slip coefficient to 2 result will be exactly the same as if both were set to 1 since 0.5*2=1*1.E (falloff)- Determines how fast curve will fall off after the peak. It depends on other parameters but in general lower value will mean that curve ends closer to 0, and value of 1 will mean that it is almost horizontal after the peak. If set to low value vehicle will start to slide once traction is lost and if set to high value there will be almost no difference between “has traction” and “lost traction” parts of the curve.